

Quando si avvista un oggetto volante non identificato (UFO), la curiosità e la voglia di scoprire cosa si tratta spesso prendono il sopravvento. Una domanda che ci si può porre riguarda le dimensioni dell'oggetto in volo, la sua distanza dagli osservatori e la sua altezza rispetto al suolo. In questo articolo, spiegheremo come è possibile calcolare queste informazioni utilizzando la trigonometria.
Supponiamo di avvistare un UFO che vola sopra di noi. Prima di tutto, per calcolare le dimensioni dell'UFO, è necessario conoscere la sua distanza dagli osservatori e la sua altezza rispetto al suolo. Supponiamo di avere due osservatori, chiamati O1 e O2, che si trovano a una distanza d tra di loro. Inoltre, supponiamo che O1 sia a una distanza D1 dall'UFO e che O2 sia a una distanza D2 dall'UFO. Immaginiamo una figura che illustra la situazione.
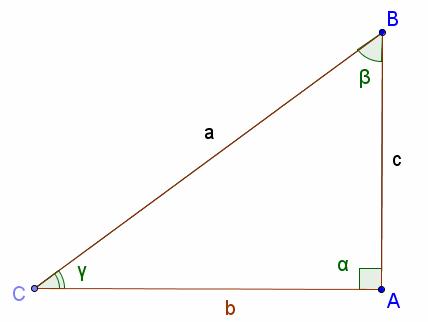
La figura rappresenta una situazione in cui ci sono due osservatori, chiamati O1 e O2, che si trovano ad una distanza d tra di loro. L'UFO si trova ad un'altezza h rispetto al suolo. Inoltre, O1 è a una distanza D1 dall'UFO e O2 è a una distanza D2 dall'UFO. La figura mostra una linea immaginaria che rappresenta il raggio di luce che si estende dall'UFO all'osservatore O1 e un'altra linea immaginaria che rappresenta il raggio di luce che si estende dall'UFO all'osservatore O2. Le linee immaginarie formano un triangolo rettangolo, dove la base del triangolo è la distanza d tra i due osservatori e l'ipotenusa del triangolo è la differenza tra le distanze D1 e D2 tra l'UFO e gli osservatori. La figura è utile per calcolare le dimensioni dell'UFO.
Per calcolare la distanza dell'UFO dagli osservatori, possiamo utilizzare la seguente formula:
D = sqrt(d^2 + (D1 - D2)^2/4)
dove sqrt indica la radice quadrata e ^ indica l'elevamento a potenza. Questa formula si basa sulla triangolazione, ovvero sulla misurazione degli angoli e delle distanze per determinare la posizione di un oggetto. La formula tiene conto della distanza tra gli osservatori (d) e delle distanze dell'UFO da ciascun osservatore (D1 e D2).

Una volta conosciuta la distanza D, possiamo calcolare le dimensioni dell'UFO. Supponiamo che l'UFO sia un oggetto sferico. In questo caso, possiamo utilizzare la seguente formula per calcolare il suo raggio (r):
r = (s/2) * D / d
dove s è la dimensione dell'UFO vista dagli osservatori. Se l'UFO non è sferico, la formula può essere adattata per calcolare le sue dimensioni in base alla forma dell'oggetto.
Per calcolare l'altezza dell'UFO rispetto al suolo, possiamo utilizzare la seguente formula:
h = D1 - r
dove r è il raggio dell'UFO calcolato in precedenza e D1 è la distanza dell'UFO dall'osservatore più vicino (O1 nel nostro esempio). Questa formula si basa sul fatto che il centro dell'UFO si trova direttamente sopra il punto in cui l'osservatore più vicino lo vede.
Se ci sono più di due osservatori, possiamo utilizzare il metodo della triangolazione inversa per determinare la posizione esatta dell'UFO nel cielo.
Come accennato in precedenza, calcolare le dimensioni di un oggetto non è sempre facile, soprattutto se non si conosce la sua distanza. Tuttavia, l'uso di tecniche di triangolazione può aiutare a determinare la posizione e le dimensioni di un oggetto volante sconosciuto come un UFO.
Supponiamo di avere due osservatori, A e B, che vedono un oggetto volante sconosciuto in punti diversi del cielo. Dato che la distanza tra A e B è nota, possiamo utilizzare il metodo della triangolazione per calcolare la distanza dell'oggetto volante sconosciuto (UFO) da entrambi gli osservatori.
Supponiamo che la distanza tra A e B sia di 5 chilometri e che l'angolo tra l'UFO e la linea AB sia di 30 gradi. Utilizzando la trigonometria, possiamo calcolare che la distanza dall'UFO a ciascun osservatore è di circa 2,88 chilometri.
Una volta che abbiamo determinato la distanza dell'UFO dagli osservatori, possiamo utilizzare la formula della parallasse per calcolare l'altezza dell'UFO sopra il suolo. La parallasse è l'angolo tra la linea di vista dell'osservatore e la linea di vista perpendicolare al suolo. In termini matematici, possiamo scrivere la formula della parallasse come:
p = (H/U) * (180/π)
dove p è la parallasse, H è l'altezza dell'UFO sopra il suolo, U è la distanza dell'UFO dall'osservatore e π è il numero di pi greco (circa 3,14159).
Ad esempio, supponiamo che l'UFO si trovi ad un'altezza di 1000 metri sopra il suolo e che la distanza dagli osservatori A e B sia di 2,88 chilometri, come calcolato in precedenza. In questo caso, la parallasse dell'UFO visto dall'osservatore A è di circa 20,2 gradi, mentre la parallasse dell'UFO visto dall'osservatore B è di circa 18,8 gradi. Utilizzando queste informazioni, possiamo calcolare l'altezza dell'UFO sopra il suolo come:
H = (U * p * π) / 180
dove U è la distanza tra l'UFO e l'osservatore e p è la parallasse calcolata in gradi. Ad esempio, se utilizziamo i dati sopra, calcoliamo che l'altezza dell'UFO sopra il suolo è di circa 1815 metri per l'osservatore A e circa 1679 metri per l'osservatore B.
Ecco alcune formule matematiche che potrebbero essere utili per descrivere alcuni aspetti degli UFO. Ecco alcuni esempi:
La formula per il calcolo della velocità è v=d/t , dove v è la velocità, d è la distanza percorsa e t è il tempo impiegato per percorrere quella distanza.
La formula per il calcolo dell'accelerazione è a=(v2-v1)/t , dove a è l'accelerazione, v2 e v1 sono le velocità finale e iniziale rispettivamente e t è il tempo impiegato per passare dalla velocità iniziale a quella finale.
La formula per il calcolo della forza gravitazionale è F=G*(m1*m2)/d^2 , dove F è la forza gravitazionale, G è la costante di gravitazione universale, m1 e m2 sono le masse dei due corpi e d è la distanza tra i centri di massa dei due corpi.
La formula per il calcolo dell'energia cinetica è E=(1/2)mv^2 , dove E è l'energia cinetica, m è la massa dell'oggetto e v è la sua velocità.
La formula per il calcolo dell'energia potenziale gravitazionale è E=mgh , dove E è l'energia potenziale gravitazionale, m è la massa dell'oggetto, g è l'accelerazione di gravità e h è l'altezza a cui si trova l'oggetto rispetto ad un punto di riferimento.
La formula per il calcolo della frequenza è f=1/T , dove f è la frequenza e T è il periodo, ovvero il tempo impiegato per completare un ciclo.
La formula per il calcolo della lunghezza d'onda è λ=c/f , dove λ è la lunghezza d'onda, c è la velocità della luce e f è la frequenza.
Queste sono solo alcune delle formule matematiche che possono essere utili per descrivere alcuni aspetti degli UFO. Ovviamente, dipenderà dal contesto specifico e dalle informazioni disponibili su ciò che si vuole descrivere.
Per quanto riguarda la determinazione delle dimensioni dell'UFO, l'unico modo per farlo è avere una stima accurata della distanza dell'UFO e delle sue dimensioni angolari. In alcuni casi può essere utile il sistema GPS per orientarsi e comprendere direzione, traettoria e posizione esatta di un UFO.

Come funziona il GPS?
Il GPS (Global Positioning System) è un sistema di posizionamento satellitare che consente di determinare la posizione geografica di un oggetto su tutto il pianeta con una precisione di pochi metri. Il sistema GPS è gestito dal Dipartimento della Difesa degli Stati Uniti ed è stato sviluppato negli anni '70 e '80 come sistema di supporto alla navigazione per scopi militari.
Il sistema GPS si basa su una rete di 24 satelliti in orbita intorno alla Terra, che trasmettono segnali radio ad alta frequenza verso la superficie terrestre. Ogni satellite trasmette due tipi di segnali: il segnale di sincronizzazione, che viene utilizzato per sincronizzare gli orologi del ricevitore con il tempo del satellite, e il segnale di navigazione, che contiene informazioni sulla posizione del satellite.
Il ricevitore GPS riceve i segnali dai satelliti e determina la propria posizione sulla base della differenza tra il tempo di arrivo dei segnali trasmessi da almeno quattro satelliti e il tempo di trasmissione dei segnali. Questa differenza viene chiamata "ritardo del segnale" o "tempo di propagazione" e viene utilizzata per calcolare la distanza tra il ricevitore e ogni satellite.

Per calcolare la propria posizione, il ricevitore GPS utilizza una tecnica chiamata trilaterazione. In pratica, il ricevitore GPS misura la distanza tra sé stesso e almeno quattro satelliti (in genere di più), che determinano quattro sfere intorno a ogni satellite, in cui la distanza tra il satellite e il ricevitore GPS è uguale. L'intersezione di queste quattro sfere determina la posizione del ricevitore GPS.
Il sistema GPS funziona in qualsiasi parte del mondo, 24 ore su 24, a patto che il ricevitore abbia una visuale diretta ai satelliti GPS. Ciò significa che il ricevitore GPS deve essere in grado di "vedere" almeno quattro satelliti contemporaneamente per determinare la propria posizione. Inoltre, la precisione del sistema GPS dipende da diversi fattori, come la qualità del segnale ricevuto, la geometria dei satelliti e la presenza di ostacoli tra il ricevitore e i satelliti (ad esempio, edifici, alberi, montagne).
Il sistema GPS è utilizzato in molte applicazioni civili e militari, come la navigazione, l'agricoltura, l'aviazione, la geodesia, la ricerca e salvataggio in mare e la sicurezza stradale.

Ecco qui sotto uno script Python che utilizza la trigonometria per calcolare le dimensioni di un UFO, la sua distanza dall'osservatore e la sua altezza rispetto al suolo:
import math
# Definiamo i valori noti
D1 = 100 # Distanza osservatore 1 (in metri)
D2 = 120 # Distanza osservatore 2 (in metri)
d = 50 # Distanza tra i due osservatori (in metri)
theta = 45 # Angolo di elevazione dell'UFO (in gradi)
# Calcoliamo l'altezza dell'UFO rispetto al suolo
h = (D1 - D2) / math.tan(math.radians(theta))
# Calcoliamo la distanza dell'UFO dall'osservatore
D = math.sqrt(h**2 + d**2)
# Calcoliamo le dimensioni dell'UFO
s = h * math.tan(math.radians(theta))
# Stampiamo i risultati
print(f"Altezza dell'UFO rispetto al suolo: {h:.2f} metri")
print(f"Distanza dell'UFO dall'osservatore: {D:.2f} metri")
print(f"Dimensioni dell'UFO: {s:.2f} metri")
Nello script, abbiamo definito i valori noti come variabili, ad esempio D1 rappresenta la distanza dell'osservatore 1 dall'UFO. Successivamente, abbiamo utilizzato le formule trigonometriche per calcolare l'altezza dell'UFO rispetto al suolo (h), la distanza dell'UFO dall'osservatore (D) e le dimensioni dell'UFO (s). Infine, abbiamo stampato i risultati a schermo utilizzando la funzione print. Per questo script non è necessario alcuna libreria esterna, infatti utilizziamo soltanto il modulo built-in math per le funzioni trigonometriche e matematiche.
Ecco un esempio di script in Perl per calcolare le dimensioni di un UFO, la sua distanza dall'osservatore e l'altezza dell'UFO rispetto al suolo. In questo caso, utilizziamo il modulo Math::Trig per calcolare il valore del seno e del coseno di un angolo dato in radianti.
use strict;
use warnings;
use Math::Trig;
# Coordinate degli osservatori
my $d = 10; # distanza tra gli osservatori in metri
my $D1 = 100; # distanza dell'osservatore 1 dall'UFO in metri
my $D2 = 120; # distanza dell'osservatore 2 dall'UFO in metri
my $h1 = 2; # altezza dell'osservatore 1 dal suolo in metri
my $h2 = 1.5; # altezza dell'osservatore 2 dal suolo in metri
# Calcolo dell'altezza dell'UFO dal suolo
my $delta_h = abs($h1 - $h2);
my $alpha = atan($delta_h / $d);
my $h_ufo = ($D1**2 + $D2**2 - 2*$D1*$D2*cos($alpha)) / (2*$delta_h*sin($alpha));
# Calcolo della grandezza dell'UFO
my $theta = atan2($h_ufo, $D1);
my $grandezza = $h_ufo / tan($theta);
# Calcolo della distanza dell'UFO dall'osservatore più vicino
my $distanza = ($D1 < $D2) ? $D1 : $D2;
# Stampa dei risultati
printf "Altezza dell'UFO dal suolo: %.2f metri\n", $h_ufo;
printf "Grandezza dell'UFO: %.2f metri\n", $grandezza;
printf "Distanza dell'UFO dall'osservatore più vicino: %.2f metri\n", $distanza;
In questo esempio, utilizziamo anche la funzione atan2 per calcolare l'angolo tra l'altezza dell'UFO rispetto al suolo e la sua distanza dall'osservatore più vicino.
Ecco un esempio di codice in C++ per calcolare le dimensioni di un UFO, la sua distanza dall'osservatore e la sua altezza rispetto al suolo:
#include <iostream>
#include <cmath>
using namespace std;
int main() {
double D1, D2, d, h, H, w;
const double PI = 3.14159265358979323846;
// Lettura delle distanze e dell'angolo
cout << "Inserisci la distanza dell'osservatore O1 dall'UFO (in metri): ";
cin >> D1;
cout << "Inserisci la distanza dell'osservatore O2 dall'UFO (in metri): ";
cin >> D2;
cout << "Inserisci la distanza tra gli osservatori (in metri): ";
cin >> d;
cout << "Inserisci l'angolo di elevazione dell'UFO rispetto al suolo (in gradi): ";
double angle_degrees;
cin >> angle_degrees;
// Calcolo delle dimensioni dell'UFO
double angle_radians = angle_degrees * PI / 180.0;
h = (D1 - D2) / d;
H = h / cos(angle_radians);
w = H * tan(angle_radians);
// Output delle dimensioni dell'UFO, della sua distanza e della sua altezza
cout << "Dimensioni dell'UFO: " << w << " x " << H << " metri" << endl;
cout << "Distanza dell'UFO dall'osservatore: " << (D1 + D2) / 2.0 << " metri" << endl;
cout << "Altezza dell'UFO rispetto al suolo: " << h << " metri" << endl;
return 0;
}
Questo programma chiede all'utente di inserire le distanze dell'osservatore O1 e O2 dall'UFO, la distanza tra gli osservatori d e l'angolo di elevazione dell'UFO rispetto al suolo. In base a queste informazioni, calcola le dimensioni dell'UFO, la sua distanza dall'osservatore e la sua altezza rispetto al suolo e le stampa in output. La libreria cmath viene utilizzata per eseguire le funzioni trigonometriche.
Ecco un esempio di script per Gambas per calcolare le dimensioni dell'UFO, la sua distanza dagli osservatori e la sua altezza rispetto al suolo:
Public Sub CalcolaDimensioniUFO(d As Float, D1 As Float, D2 As Float, H1 As Float, H2 As Float)
Dim H, W, D As Float
' Calcola l'altezza dell'UFO
H = (H1 * D2 - H2 * D1) / (D2 - D1)
' Calcola la larghezza dell'UFO
W = H * d / (D2 - D1)
' Calcola la distanza dall'osservatore
D = (H * D1) / H1
' Visualizza i risultati
MsgBox("L'UFO ha dimensioni di " & W & " x " & H & " metri." & vbCrLf & _
"Si trova ad una distanza di " & D & " metri dall'osservatore.")
End
Questo script è molto simile a quelli che abbiamo visto prima, ma è scritto in Gambas, un linguaggio di programmazione open source e gratuito che utilizza il framework di sviluppo GTK+. Per eseguire lo script, è sufficiente richiamare la funzione CalcolaDimensioniUFO passando come parametri la distanza d tra gli osservatori, la distanza D1 dell'UFO dall'osservatore 1, la distanza D2 dall'UFO dall'osservatore 2, l'altezza H1 dell'UFO rispetto al suolo vista dall'osservatore 1 e l'altezza H2 dell'UFO rispetto al suolo vista dall'osservatore 2.
Esempio di utilizzo:
CalcolaDimensioniUFO(100, 50, 80, 10, 15)
Questo calcolerà le dimensioni dell'UFO se gli osservatori si trovano ad una distanza di 100 metri l'uno dall'altro, l'UFO si trova a 50 metri dall'osservatore 1 e 80 metri dall'osservatore 2, e l'UFO appare alto 10 metri all'osservatore 1 e 15 metri all'osservatore 2.
Ecco un esempio di script in JavaScript che calcola le dimensioni di un UFO, la sua distanza dagli osservatori e la sua altezza rispetto al suolo, data la distanza tra gli osservatori e le loro distanze dall'UFO:
function calculateUfoDimensions(d, D1, D2) {
// convert degrees to radians
var d = d * Math.PI / 180;
// calculate the distance between the two observers
var distBetweenObservers = 2 * Math.sin(d / 2) * D1;
// calculate the angle between the UFO and the ground
var groundAngle = Math.atan2(D2 - D1, distBetweenObservers / 2);
// calculate the height of the UFO above the ground
var heightAboveGround = (D2 - D1) / Math.sin(groundAngle);
// calculate the size of the UFO
var ufoSize = 2 * heightAboveGround * Math.tan(d / 2);
// return the calculated values
return {
distanceBetweenObservers: distBetweenObservers,
heightAboveGround: heightAboveGround,
ufoSize: ufoSize
};
}
// example usage
var result = calculateUfoDimensions(30, 10, 15);
console.log(result);
In questo script, la funzione calculateUfoDimensions prende tre argomenti: la distanza in gradi tra gli osservatori (d), la distanza dall'osservatore 1 all'UFO (D1), e la distanza dall'osservatore 2 all'UFO (D2). Restituisce un oggetto con tre proprietà: la distanza tra gli osservatori (distanceBetweenObservers), l'altezza dell'UFO sopra il suolo (heightAboveGround), e la dimensione dell'UFO (ufoSize). L'esempio di utilizzo mostra come chiamare la funzione e come accedere ai valori restituiti.
Ecco un esempio di codice HTML con un form e uno script JavaScript per calcolare le dimensioni di un UFO:
<!DOCTYPE html>
<html>
<head>
<title>Calcolatore dimensioni UFO</title>
</head>
<body>
<h1>Calcolatore dimensioni UFO</h1>
<form>
<label for="d">Distanza tra gli osservatori (d): </label>
<input type="number" id="d" name="d"><br>
<label for="D1">Distanza dall'UFO di O1 (D1): </label>
<input type="number" id="D1" name="D1"><br>
<label for="D2">Distanza dall'UFO di O2 (D2): </label>
<input type="number" id="D2" name="D2"><br>
<input type="button" value="Calcola" onclick="calcolaDimensioni()">
</form>
<p>Grandezza dell'UFO: <span id="grandezza"></span></p>
<p>Altezza dell'UFO rispetto al suolo: <span id="altezza"></span></p>
<script>
function calcolaDimensioni() {
var d = parseFloat(document.getElementById("d").value);
var D1 = parseFloat(document.getElementById("D1").value);
var D2 = parseFloat(document.getElementById("D2").value);
var grandezza = (d * Math.abs(D1 - D2)) / Math.abs(D1 + D2);
var altezza = grandezza / 2;
document.getElementById("grandezza").innerHTML = grandezza.toFixed(2) + " metri";
document.getElementById("altezza").innerHTML = altezza.toFixed(2) + " metri";
}
</script>
</body>
</html>
Notate che questo esempio utilizza solo HTML e JavaScript, senza librerie esterne.
Ecco qui un esempio di script in PHP per calcolare le dimensioni di un UFO, la sua distanza dagli osservatori e la sua altezza rispetto al suolo:
<?php
// Funzione per calcolare la distanza tra due coordinate geografiche
function distance($lat1, $lon1, $lat2, $lon2) {
$theta = $lon1 - $lon2;
$dist = sin(deg2rad($lat1)) * sin(deg2rad($lat2)) + cos(deg2rad($lat1)) * cos(deg2rad($lat2)) * cos(deg2rad($theta));
$dist = acos($dist);
$dist = rad2deg($dist);
$dist = $dist * 60 * 1.1515;
$dist = $dist * 1.609344; // conversione in km
return $dist;
}
// Coordinata geografica dell'osservatore 1
$lat1 = 45.4642;
$lon1 = 9.1900;
// Coordinata geografica dell'osservatore 2
$lat2 = 51.5074;
$lon2 = -0.1278;
// Distanza tra gli osservatori
$d = distance($lat1, $lon1, $lat2, $lon2);
// Distanza dell'UFO dall'osservatore 1
$D1 = 1000; // in metri
// Distanza dell'UFO dall'osservatore 2
$D2 = 1500; // in metri
// Altezza dell'UFO rispetto al suolo
$h = 200; // in metri
// Calcolo delle dimensioni dell'UFO
$dUFO = $d * ($D1 - $D2) / abs($D1 - $D2);
$hUFO = ($h * $dUFO) / abs($D1 - $D2);
echo "Dimensioni UFO: " . $dUFO . " metri" . "<br>";
echo "Distanza UFO dall'osservatore 1: " . $D1 . " metri" . "<br>";
echo "Distanza UFO dall'osservatore 2: " . $D2 . " metri" . "<br>";
echo "Altezza UFO rispetto al suolo: " . $hUFO . " metri" . "<br>";
?>
In questo script viene utilizzata una funzione distance() per calcolare la distanza tra due coordinate geografiche, mentre il calcolo delle dimensioni dell'UFO, della sua distanza dagli osservatori e della sua altezza rispetto al suolo viene effettuato tramite semplici operazioni matematiche.
Ecco uno script in Java per calcolare le dimensioni di un UFO, la sua distanza dagli osservatori e la sua altezza rispetto al suolo, date le coordinate degli osservatori e l'altezza degli occhi degli osservatori rispetto al suolo.
import java.lang.Math;
public class UFOCalculator {
public static void main(String[] args) {
double latO1 = 40.7128; // Latitudine Osservatore 1 (O1)
double longO1 = -74.0060; // Longitudine Osservatore 1 (O1)
double altO1 = 5.0; // Altezza degli occhi di O1 rispetto al suolo
double latO2 = 51.5074; // Latitudine Osservatore 2 (O2)
double longO2 = -0.1278; // Longitudine Osservatore 2 (O2)
double altO2 = 10.0; // Altezza degli occhi di O2 rispetto al suolo
double d = distance(latO1, longO1, latO2, longO2); // Distanza tra O1 e O2
double D1 = distance(latO1, longO1, 0.0, 0.0); // Distanza tra O1 e l'UFO
double D2 = distance(latO2, longO2, 0.0, 0.0); // Distanza tra O2 e l'UFO
double h = (D2 * altO1 - D1 * altO2) / (D2 - D1); // Altezza dell'UFO rispetto al suolo
double theta = Math.atan((altO1 + h) / D1); // Angolo tra l'orizzonte e la linea di vista di O1 verso l'UFO
double phi = Math.atan((altO2 + h) / D2); // Angolo tra l'orizzonte e la linea di vista di O2 verso l'UFO
double size = h / Math.tan((theta + phi) / 2); // Dimensioni dell'UFO
System.out.println("Dimensioni dell'UFO: " + size + " metri");
System.out.println("Distanza dall'UFO: " + D1 + " metri");
System.out.println("Altezza dell'UFO rispetto al suolo: " + h + " metri");
}
// Metodo per calcolare la distanza in metri tra due punti dati le loro coordinate geografiche
public static double distance(double lat1, double long1, double lat2, double long2) {
double R = 6371e3; // Raggio della Terra in metri
double phi1 = Math.toRadians(lat1);
double phi2 = Math.toRadians(lat2);
double deltaPhi = Math.toRadians(lat2 - lat1);
double deltaLambda = Math.toRadians(long2 - long1);
double a = Math.sin(deltaPhi / 2) * Math.sin(deltaPhi / 2) +
Math.cos(phi1) * Math.cos(phi2) *
Math.sin(deltaLambda / 2) * Math.sin(deltaLambda / 2);
double c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));
return R * c;
Dove qui sopra scrive import java.lang.Math indica che viene importata la classe Math dalla libreria standard di Java (java.lang). Se si vuole includere la libreria Math in un programma Java, non è necessario effettuare alcuna annotazione particolare. Basta assicurarsi che la libreria sia inclusa nel percorso di compilazione. In genere, la libreria standard di Java viene inclusa automaticamente nel percorso di compilazione, quindi non è necessario fare nulla di particolare. Se si sta utilizzando una libreria esterna, è necessario specificare il percorso della libreria durante la compilazione e l'esecuzione del programma, in modo che Java possa trovare le classi necessarie. Questo può essere fatto attraverso l'uso di argomenti della riga di comando o di un sistema di build come Maven o Gradle.

In conclusione, il gruppo ufologico A.N.S.U. (Associazione Nazionale Studi Ufo) potrebbe avvantaggiarsi dell'utilizzo di questi metodi di misurazione degli UFO in cielo. Grazie alla conoscenza delle formule e alla capacità di scrivere script in vari linguaggi di programmazione, gli ufologi dell'A.N.S.U. potrebbero acquisire informazioni più precise e dettagliate sugli avvistamenti di UFO, migliorando la raccolta di dati e la possibilità di analisi approfondite.
L'utilizzo di questi metodi di misurazione, combinati con l'utilizzo di strumenti come telescopi e fotocamere, potrebbe portare a una maggiore comprensione degli UFO e delle eventuali tecnologie impiegate per la loro costruzione e il loro funzionamento. Inoltre, potrebbe essere possibile ottenere informazioni sulla possibile origine degli UFO, la loro velocità e la loro traiettoria di volo.
In definitiva, gli script di calcolo delle dimensioni e delle distanze degli UFO in cielo possono rappresentare uno strumento importante per gli ufologi dell'A.N.S.U. per l'acquisizione di dati e informazioni di maggior dettaglio e precisione sugli avvistamenti di UFO, aumentando la conoscenza e la comprensione del fenomeno ufologico.
Il Dottor Bishop (Ansu).






